[Printed book in 3 volumes, plus Pdf, Epub, Mobi.]

[logo]

Recovering the Lost World,
A Saturnian Cosmology -- Jno Cook
Chapter 29: The Maya Calendar.


[previous] [table of contents] [next]

$Revision: 42.32 $ (maya.php)
Contents of this chapter: [The Beginning of Time] [The First Calendar] [An Intermediate Calendar] [The Tzolkin Calendar] [Modification of the Tzolkin] [The Haab Calendar] [The Long Count] [The Katun Cycle] [The Four Ages] [Endnotes]

The Maya Calendar

The Mesoamerican / Maya calendar contains cycles within cycles, all of which are held as significant to some degree in determining the "quality" of any day in time. Many of the cyclical features look like remnants of earlier calendar systems which could not be discarded, but were carried forward in time as each change in the calendar was forced upon the users with a change in the structure of the Solar System. I would thus suggest that the current calendar -- because of its inclusion of these arcane, and in some cases near-useless, features -- shows faithful and careful adjustments to changes in the number of days in the year over a very long period. I'll suggest, in fact, that the current calendar can certainly be traced back to the era starting in 3147 BC, and likely a prior tally used solar years before 3147 BC. I think this is clearly shown by the remnants retained at later times. In fact, a page of the Chilam Balam, which deals with the events of 2349 BC, specifically states, "And then days of the year were introduced." But this is the addition of a round of 13 numbers superimposed on the original "monthly" calendar of 20 named days.

It is also certain that there was a calendar, in the sense of a count of years, going forward from (the retrocalculated year of) 3114 BC, since the Maya Chilam Balam correctly places the earliest event of the current era in the properly named double-decade Katuns.

Also, some count of years, or spans of time, was recorded since circa 41,000 bp. One of the pages of the Chilam Balam specifically deals with this.

I should also note that the Baktuns and Katuns were probably in use by 10,900 BC, for the Chilam Balam has reference to this in Book 11 which details (what we would call the start of) the "first creation" of 10,900 BC. In 8347 BC, with the end to a period of about 2500 years of the southern ball plasmoids, the count of years had reached 13 Baktuns, and the year tally was reset to zero.

It happened again in 3147 BC, with the collapse of the "Era of the Gods," that 13 Baktuns were reached. Thus in 3147 BC the Baktun measure of the calendar was again reset to zero. This marks the termination of the "Second Creation" of the Olmec and Maya, marked especially since it was accompanied by the worldwide flood. Meanwhile, Saturn had started to blaze in 4077 BC.

Note that the "Creations" are not clear-cut episodes separated by definitive collapses of celestial conditions. For example, the date of 4077 BC, when Saturn blazed up in a nova expulsion, is not accounted for. It makes one suspect that the whole idea of various numbered creations might be a constructed effort of a late date.

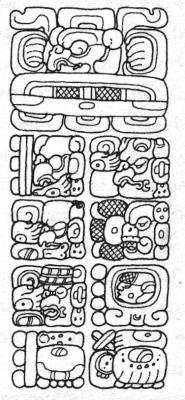
[image: August 13, 3114 BC, day
[Image: August 13, 3114 BC, day "zero" of the Maya calendar. This reads, "13 Baktun, 0 Katun, 0 Tun, 0 Uinal, 0 Kin, 4-Ahau 8-Cumku, was seen the image." After research.famsi.org.]

... preliminary observations

With the institution of the Long Count in 747 BC, the Olmecs were able to calculate backwards into the past to determine the exact names and numbers of the days on the Tzolkin calendar and Haab calendar. When the completion of the previous era was reached in 3147 BC (which they and we calculate as 3114 BC) -- the Tzolkin day was 4-Ahau and the Haab day was 8-Cumku. The Peten region Maya were very proud of this feat of retrocalculation and had reference to it constantly in their standing stone monuments.

As interpreted by archaeologists, the Long Count used August 11, 3114 BC, on an equivalent Gregorian calendar as a starting point. Because there is a two-day difference in calendars between early Olmec (and current Guatemala) and the calendar of the Maya (and Aztecs), the other widely accepted date is August 13, 3114 BC. In both cases it is assumed that the year has always been the same length as today -- 365.2422 days. The Classical era Maya (AD 400 to 700) also used this measure, arrived at independently, to suggest a series of days which never varied, and retrocalculate the Tzolkin and Haab day names and numbers at the beginning of the current creation -- even though they are incorrect. There were records involved in the recall of history, but they were not accurate.

The archaeological count of days (which match the Maya Long Count against our own erroneous string of calendar days) starts at August 11, 3114 BC. This was first derived by Joseph Goodman in 1905. Juan Hernández in 1926 came up with a calculation of August 12, which was followed in 1927 by John E. Thompson's calculation of August 13. In 1935 Thompson revised his calculation to August 11. As the dean of Maya archaeologists, Thompson's estimate is generally used today, although any number of researchers think that the date of August 13, 3114 BC, is more likely to be correct.

"Overwhelming support for the precise placement of the Thompson [August 11] correlation number came in the 40's and 50's, when newly discovered calendar counts still being followed among the Quiche, Kekchi and Ixil of Guatemala all supported the [August 11 date]."

-- John Major Jenkins at fourahau2.htm.

The above "correlation dates" are on the equivalent Gregorian calendar, converted from a measure known as the "count of Julian days" used by astronomers since the 16th century AD. The "astronomical year" for 3114 BC is -3113, based on recognizing a "year zero." The Gregorian calendar will match solar years under the assumption that the length of the year has not changed.

The Julian calendar, in use from about 40 BC to about AD 1500, and not to be confused with "Julian days," is based on a year of 365.25 days, and thus the Julian year is slightly longer than the Gregorian year of 365.24 days. By 3114 BC the Julian calendar places dates about 13 months (numerically) further into the past than the Gregorian calendar.

There have been suggestions that the Maya made a two-day correction at some time in the past, and that this accounts for the difference of two days between the Long Count notation found on monuments in antiquity, and in the continued use of the earlier Tzolkin among contemporary tribes.

In fact, Vincent H. Malmstrom, writing in Cycles of the Sun, Mysteries of the Moon (1997), suggests that this happened in circa 48 BC -- that the Maya in effect skipped two days, thus setting the calendar ahead by two days. Malmstrom sets out when and where this would have happened, and the reasoning behind the change, but admits that his "story" is pure conjecture.

A "correction" carries with it the suggestion of an absolute and uniform use of the Tzolkin and Haab calendars by many tribes spread over a large area since remote antiquity. The concept of uniform agreement doesn't work among humans. I think it should be considered that by 747 BC, when the Long Count was devised, there were already some diverse regional opinions on the concept of when one era ended and another started -- a question about the existence ("completion") of two days which had not been seen in progress. Considering that the 2000-year-old Tzolkin was in use among many diverse tribes, it is likely that some stubborn local opinions prevailed. But there might be other reasons, too.

The "August 11" calendar reaches further into the past by two days. It correctly fits the start of the Long Count on February 28, 747 BC, and accounts for later retrocalculations of some past events by the Olmecs. But it was supplanted by the "August 13" calendar because the "August 13" calendar "correctly" fit what was thought to be the quality of a number of important dates in the year 685 BC, and in 1492 BC. (Discussed in the chapter "The Day of Kan.")

My sense is that in the Valley of Mexico, and perhaps also in the Olmec coastal region, the "August 11" calendar was replaced by the "August 13" calendar by 400 BC, but long after the use of the "August 11" calendar had been exported and adapted by tribes in Southern Mexico and Guatemala, where it has been retained in the same form to today. (Some researchers have suggested that the calendars may have started in Guatemala.)

It should also be pointed out that August 11, 3114 BC (or August 13), is not the start of the current era, but is the end (the completion) of the previous era. The texts at Palenque, for example, make this clear when it is read:

"And then the past epoch ended. On 4-Ahau 8-Cumku [presumed to be August 13, 3114 BC], 13 Baktuns were completed."

The transliterated text reads:

"(And then) there was an event / (on) 4-Ahau / 8-Cumku / were completed / 13 Baktuns"

There can be little doubt, no matter how it is translated, that this phrasing speaks to the completion of a previous 13 Baktuns -- 5200 solar years. It points directly to an earlier calendar which would have started in 8347 BC. Occasional stelae specify the placement on the day 4-Ahau 8-Cumku of "the three stones" or alternately the first "image of the turtle." The references here are to a day in the year 3147 BC, but the day name and number are known only because of a retrocalculation by the Olmecs or the people of the Valley of Mexico in antiquity, probably after 600 BC, which found this day name and number for the restart of the calendar in 3147 BC, even if incorrect. It is, in fact, incorrect since the three stones or the turtle were seen to be placed in 10,900 BC.

Support for a correlation based on the date of August 13 (for the year 3114 BC) comes from the record of eclipses, which cannot be off by a day. My observation is that the starting date of February 28th, 747 BC, Gregorian, corresponding to the Long Count date of 6.0.0.0.0, can only be upheld with an "August 11" correlation. This matches the start of the Era of Nabonassar in the Eastern Mediterranean region (the evening of February 27, 747 BC) and the start of the Roman calendar (the day after February 28th). I think the arguments among archaeologists and historians may be meaningless. It should be recognized that there were two Long Counts in use, and that they differed by two days. [note 1]

The first Tzolkin date inscription was in use at the Zapotec site of San José Mogote in the Oaxaca region in about 600 BC. By 400 BC the Tzolkin and Haab calendars were in use at Monte Alban in Oaxaca.

In 1939 the earliest engraved Olmec Long Count was discovered and depicted on Stela C from Tres Zapotes as 32 BC (Julian). Malmstrom notes that this stele celebrated a total eclipse of the Sun as it rose out of the Eastern Gulf of Mexico, if the August 13 Thompson correlation is used. Otherwise it would be off by two days. Malmstrom notes a transcription error in the stele (carving three bars rather than two to accompany the three dots for the "kin") and then writes about the eclipse:

"... whose path ... passed right over the Olmec ceremonial center of Tres Zapotes at dawn on the morning of August 31, 32 B.C. A more frightening celestial event can scarcely be imagined, for the sun rose out of the Gulf of Mexico totally black except for a ring of light around its outer edges. [It was] described as an annular, or ringlike, eclipse, and subsequent calculations at the U.S. Naval Observatory have revealed that the disk of the sun was 93 percent obscured (personal communication). Surely, a 'day without a sunrise' is not likely to have gone unrecorded by the Olmecs!"

He concludes with:

"... therefore, the inscription of Stele C, erroneous though it seems to be, appears to confirm the accuracy of the original Thompson correlation value [August 13] between the Olmec calendar and our own."

Malmstrom also identifies a much later eclipse seen at Copan (Copán) on June 29, AD 763 (9.16.12.5.17 6-Caban 10-Mol), and suggests that it had been predicted. Again, the date agrees with a lunar eclipse only if the "August 13" correlation is used. The date was recorded on a half dozen stelae. Archaeologists have not as yet accepted this. (Surprise!)

It should be obvious also from many inscribed stelae that it is the completion of a time period that is celebrated, not the start. The event of 3114 BC (actually 3147 BC) is known as the end of the "second creation," which is inferred from the fact that the event which we know as the "flood of Noah" is consistently called the (completion of the) "third creation." The reason the "second creation" of 3114 BC ended with the completion of 13 Baktuns (the count of years then went to zero Baktuns), is that the predecessors of the Olmecs had already been counting years (solar years) from much earlier than 10,900 BC. In 8347 BC 13 Baktuns had been reached.

In that the Sumerians managed to have a count of years (in days) from 4077 BC, it is reasonable to suggest that the Olmecs or their predecessors were also perfectly capable of this. "Counting," after all, must have been one of the high sciences even for the slightly more remote Cro-Magnons.

The Beginning of Time

The phrase of "the image" is completed by some stelae as "the image of the turtle." As a turtle this would represent the appearance of the southern plasmoids, actually, the last appearance -- the completion of this event. We could most likely place the first showing of Peratt's southern plasmoids in 10,900 BC, the year of the first contact with Saturn at the start of the Younger Dryas which destroyed North America.

It has always been strange to note that the "zero" number for the Baktun at the start of the current era (the Maya retrocalculated 3114 BC, although actually 3147 BC) actually has a value of 13 Baktuns. Also, the date of the start of the "first creation" is not the nova event of Saturn in 4077 BC, which the Popol Vuh describes as the "dawning of the light," but an event 4000 years earlier -- the last instance of the showing of the southern ball plasmoid.

Here are the four creation periods:

The last period is questionable, it might not be over yet.

In the iconography of the Maya, the "turtle," which appeared in 10,900 BC, at the start of the "first creation," is often combined with the appearance of Jupiter ("Hun-Nal-Ye") as the "First Father" in 2349 BC, at the end of the "third creation." Just like the second and third southern plasmoids would seem to have appeared out of the carapace of the "First Turtle" soon after 10,900 BC, so First Father is shown to rise out of a turtle carapace in 2349 BC, assisted by Hunahpu and Xbalanque (from the era of the 7th century BC, no less). This scene is repeatedly shown on bowls and vases. And this is how the mythological history of the Maya advanced.

In Maya Cosmos Freidel and Schele present the imagery of a painted pot showing six Gods in council with a elderly seventh God. The council is urging the seventh god to "bring into existence" and "put in order" the place called "black is its center" -- a fit description of the deep shadow at the center of the Absu which changed size and shape over the year. It suggests that the dark doorway of the Absu was hiding something.

The elder God (God L) of the painted pot is easily identified as Jupiter as well as First Father. The six Gods have various names, of which some are easily identified. God "Three Born Together" is obviously the three plasmoids of the south and God "Nine Footsteps" is Mars. Subtracting God "Three Born Together" of the south leaves five Gods all associated with the polar configuration of the north. This is the same number as listed in the Popol Vuh (see the chapter "The Popol Vuh" for details). These are Uranus, Neptune, Saturn, Mercury, and Mars, all of which were easily distinguished in the earliest time after 9500 BC, although some disappeared behind (or above) each other by 5800 BC. And Mercury is misnamed for Venus, which probably did not exist as early as this council is meant to depict. God L (Jupiter) is here distinguished from the polar configuration planets, and it is a rare insight to suggest that indeed at the time of the council, sometime before 8347 BC, Jupiter had been known and seen for eons, and therefore was properly represented as very old.

This illustrated pot also points up the Mesoamerican concept of the simultaneity of time. The council of the six Gods happens after the start of the "first creation" period after 10,900 BC as told by the Popol Vuh, resulting eventually in the creation of the Sun -- the lighting up of Saturn. But the disposition of the dark spot -- the cleft -- in the Absu, in fact the whole of the Absu, is not tackled until the end of the "third creation" of 2349 BC. Most of the six Gods had long since disappeared from view by then. Archaeologists today think that the "dark spot" is a dark area of the cloud of stars of the Milky Way.

The other (and more common) image which is often represented as first appearing on 4-Ahau 8-Cumku, is the setting of the three hearthstones in the sky. These have been identified by Schele as a star of the belt of Orion and two of his feet (Alnitac, Rigel, and Saiph). The cluster M-42 is enclosed in this triangle, like a fire at the center of a three-stone hearth. The constellation is below (slightly east) of the intersection of the equatorial and ecliptic, and removed from the brightness of the Milky Way. In fact, these stars first showed up in 2349 BC, the date of the end of the "third creation," at a location known as "Lying-down-Sky" which must represent the gap in the Absu during the equinoxes. Other names for the shadow gap in the Absu are the "Earth Partition," "Black is the Center," and "Cleft Sky" -- the name for Yaxchilan. Where the Earth shadow fell on the Absu, no stars would have been seen in the dark area (excepting a few very bright stars).

Since the skies have been invariant since even before 10,900 BC the three hearthstones could not refer to the end of the second creation ending in 3147 BC, but to the first creation ending in 8347 BC. As stars, these three stones were not placed; they were always there, although not seen until some time after 2349 BC. This would suggest to me that the "setting of the three stones" probably refers back to the "first creation" when the three southern plasmoids appeared in the south -- set beneath the "mighty stone" (Saturn) of the north, as the Chilam Balam relates in Book 11.

The date of 3147 BC is actually a reasonable estimate for the start of the near-current era, that is, as the date for the close of the "Era of the Gods" and the end of the second 13 Baktun cycle of sets of 400 years (5200 years). The Olmecs must have had a record of the number of solar years which had lapsed since various worldwide events, and were certainly able to place events in named year tallies after 3147 BC. The records of the Chilam Balam books of the colonial-period Maya are accurate to the Katun (20-Tun period) after 3147 BC, allowing for some slight-of-hand by the 16th-century-AD Maya scribes, who made some unwarranted "corrections" to the chronology.

Time spans between "ages" (after 3147 BC) show up in later Mesoamerican legendary histories and are correct or nearly correct, and match the records of other civilizations. No clear record of events or time spans shows up among the sparse Mesoamerican records of the much earlier period before 3147 BC, except as might be inferred from their calendar measures.

When the Long Count was established in 747 BC by the Olmecs, they added six Baktuns (2400 Tun years) to a starting calendar date of 0.0.0.0, based on the assumption that the year (the Tun) had always consisted of 360 days. This was correct at that time, because the year had indeed consisted of 360 days since the establishment of earliest Olmec ceremonial center after 1500 BC (San Lorenzo). Thus the Olmecs also removed from the Long Count calculation the five-day correction that was added to the annual Haab calendar in 747 BC -- the "years" in the Long Count are based entirely on the earlier 360-day intervals, not on 365-day intervals. The rather arbitrary addition of 2400 Tuns (six Baktuns of 400-Tun years) to the Long Count would bring the actual "zero" date to 3147 BC, off from the archaeologically and Classic Maya retrocalculated date of 3114 BC year by 34 years. [note 2]

A "Tun" is a year. Before 3147 BC (the thousand years of the "Era of the Gods" and the 4000 years before that) the Tun was 225 days (I have assumed). After 3147 BC (the worldwide flood) the Tun was 240 days. After 2349 BC (the "flood of Noah") the Tun was 260 days. After 2193 BC (the fall of Akkad and the Old Kingdom) the Tun was 273 days. After 1492 (the Exodus and the fall of the Middle Kingdom) the Tun was 360 days -- and at this value it remained in its Long Count use, even though 5 additional days were added to the year after 747 BC when the year changed to its current value. Although the earlier "years" were shorter, the effect of adding 2400 Tuns (6 Baktun) was to have a calendar which reflected solar years, and is thus nearly identical to the accepted (scientific) chronology -- which assumes that all years in the past were Gregorian years of 365.2422 days.

When researchers calculate backwards to 3114 BC, using an actual count of days, they use a 365.2422-day Gregorian year. The researchers and archaeologists thus end up being able to place events in certain "years" which will match the intent of the Olmec and Maya Long Counts. Both are in error in terms of the actual number of days before 747 BC, but both are nearly correct in terms of "years" if these represented solar years. Both are in error because the later Maya also ignored the fact that the Olmecs knew the length of the year had been 360 days prior to 747 BC, and, in fact, designed the Long Count to tally in 360-day Tuns, not 365-day Haab years.

I have no problem with the suggestion that history might have been remembered from long before 3147 BC, or that some aspects of the Mesoamerican calendar date back to 2349 BC, and the count of years dates from before 10,900 BC. After all, in Northern Mesopotamia people had been accounting for trade products since about 8000 BC, and kept track of the number of days since 4077 BC. [note 3]

Mesoamerican iconography seems to spring to life sometime around 1500 to 1200 BC without any sign of a developmental phase. These are the dates of the first images carved in stone or engraved on celts. This suggests that the stone carvings were preceded by a long period of works in wood and other perishable materials, a period possibly lasting thousands of years. As an example of how long records could last, note that the Dresden Codex, a book on plaster-coated tree bark, was transcribed in about AD 1200 from material dating to before AD 700. It was sent to Spain after AD 1550. Such long endurance of books suggests the possibility of other records dating from more remote antiquity -- including, of course, chronological records.

Over the following few paragraphs I will speculate about possible early calendars, although after 2349 BC the use of a day and month calendar is certain. In circa 2350 BC Yao, the first "emperor" of China corrects the calendar. In the Enuma Elish, dating from Babylon sometime after 2000 BC, but detailing events in 2349 BC, the God Marduk does the same. Both of these instances assume there was an earlier calendar.

The First Calendar

I have estimated that before 3147 BC the year was 225 days long (see Appendix A, "Notes on Chronology"). A very simple but sophisticated calendar system could have been in use: the year was divided into 9 groups of 25. Fingers of one hand could be used to count up to 4. When 5 was reached the other hand closes a finger -- representing 5. Thus the other hand could hold a total of 25 units. The "Nine Lords of the Night" rotated nine times through the sets of 25 to count to a total of 225 days.

I am using the five fingers because both Olmec and Mayan ciphers were represented in base 5. The "Nine Lords of the Night" were still being counted 5000 years later, and still rotated endlessly through nine names. [note 4]

The "Nine Lords of the Night" together with the 25 "day numbers" (or more likely "day names") would produce 225 unique names for the days of the year. This sort of system would constitute a calendar which might have been a model for the later Tzolkin, which rotated 13 numbers against 20 names.

Who the "Nine Lords of the Night" were, or what they represented at the time before 3147 BC, is unknown. I suspect, on the basis of other sources, that the "Nine Lords of the Night" represented Jupiter and the eight nearest satellites, visible at close range after 3147 BC. Jupiter was known as "The Nine." See the chapter "The Chilam Balam" for this.

The "Nine Lords" might also represent an assignment of nine gods to the nine rings of the Absu -- the House of Nine Bushes. These would show at night (and not likely be very bright during the day).

left hand: 1 through 4
right hand: 5 through 25
9 Lords of the night (9 x 25 = 225 days)

An Intermediate Calendar

Of course, the previous is speculation. But for the period after 3147 BC, we can be much more certain of a calendar. After 3147 BC the year was (I suspect) 240 days long. The 240 days could be counted as multiples of 20 and could be made to fit 240 if 12 sets of 20 were to be used. A lunar calendar might be suggested for this era, with the period of the Moon at 20 days, but there was as yet no Moon. There is not a single suggestion of lunar calendars anywhere in the world before 2349 BC. It is more likely that the 20-day periods represented agricultural periods. It is possible that the 20 "day names" were rotated against 12 "day numbers" -- which would give 240 unique date-names to the year. [note 5]

The Mayan word for the 20 days is "uinal" which translates as "moon" and means "month." It also means "person," since a count of 20 day names could be understood as addressing all a person's fingers and toes. This person became personified as a "time-lord" who brought in the month as a parcel. Because of some such metaphorical construction, the continuity of time for Mesoamerican people was never a certainty (as it is for us) -- the bearer of time might not arrive with his burden.

The "Nine Lords of the Night" -- whatever their value might be -- remained in use.

A Person: 20 digits and toes (day names)
12 Day Numbers (20 x 12 = 240 days)
9 Lords of the Night

The Tzolkin Calendar

After 2349 BC the year went to 260 days. At this point speculation stops, although I have reached a year length of 260 days by somewhat of a circular argument (in Appendix A, "Notes on Chronology"). A line of a page of the Books of the Chilam Balam, dealing with the events of 2349 BC, reads:

"And then days of the year were introduced."

There certainly was a calendar in use, dating back some 3700 years, as the Books of the Chilam Balam show. This calendar consisted of a rotation through twenty named days. Only the preexistence of the twenty named days makes sense in the subsequent introduction of the Tzolkin calendar.

The count of days, the 260-day calendar known as the Tzolkin, as instituted in 2349 BC, was a lunar calendar. The Moon was intercepted in or after 2349 BC (see the chapter "The Day of the Dead"), and was probably in a stable orbit within a few years. Mesoamerica started to rotate 13 new "day numbers" against the existing 20 "day names" to yield 260 uniquely named days constituting a year. Brilliant! Every day of the year was individually identified and each was different from the others.

[Image: Tzolkin Calendar]
[Image: 20 Day Names of the Tzolkin Calendar. After Linda Schele and David Freidel "A Forest of Kings" (1990).]

It is unlikely that the period of the Moon was 20 days at this time, or that there were 13 months to the year. More likely the number 13 is a count of a half moon period -- from a new moon to a full moon, and back. Thus the period of the Moon was likely 26 days and there were 10 lunar months of 26 days in the year, and 20 half months of 13 days.

Typical of Mesoamerican thinking, it was the completion of a change to a full moon or the finish of the waning to a new moon that counted -- 13 days for each. Thousands of years later, the Maya still call the 20-day period a "month," and a "moon" -- but not the 13-day period. This actually seems strange if the Moon's period was 26 days.

Anyway, each of the twenty days of the Tzolkin "moon period" had a separate name -- Imix, Ik, Akbal, Kan, etc. The glyphs for the day-names are unique from other glyphs in that all twenty are graphically represented as figures of some sort within the frame of an escutcheon seated on three feet. Some of the glyphs have not been recognized, which probably speaks to their extreme antiquity, as does the whole of the arcane nature of this calendar system. Glyphs which are known include tropical plants and animals as the environment of the location where these names were first selected. It has been suggested that these escutcheons are equivalent to the Egyptian name-cartouche used for the names of pharaohs and Gods. The three feet below the frame have been identified as a rope knot (Morley). Thus the escutcheons date from 2860 BC, and can be equated to the "shen" form in Egypt.

This system of a day count which rotates endlessly through 260 number-name combinations is actually the best evidence that an earlier calendar had existed. If the Lords of the Night were kept in use since 3147 BC, then there was probably a similar pressure to retain the day names after they became obsolete because they had constituted the base of a previous calendar.

Today the Tzolkin (which is still in use) shows no concern with time as a linear progression, only as a repeating cycle. This is endemic to the Mesoamerican languages, which understand time in topological terms, rather than a linear and endless series. An "historical awareness" in terms of understanding time as a linear progression does not take hold for another 2000 years. Mayan words for time involve references to round things, circles, and cycles. The future is expressed as going from here to there, as if invoking geography. We do this also, mentally, but our geography of time is a single line with no beginning or end.

The Tzolkin calendar makes no sense to us, who are used to a completely different method of tallying days. But it fits in with the suggested earlier calendar which rotated the "Nine Lords of the Night" against day names. The strangest aspect of the Tzolkin is that the 13 numbers are rotated against the 20 names, rather than "numbering" each of the names in a sequence of 1 to 13. Perhaps stranger still is that any group of 20 are known as a "month," although this may be because of the design of the later Haab calendar.

The languages of Mesoamerican people did not use tense (serial time) in verbs, but only the sense of "on-going" and "completed." In this manner the cycling of 1-Imix, 2-Ik, and 3-Akbal makes some sense, because to count 1-Imix, 1-Ik, and 1-Akbal would leave the moon-period uncompleted until the 13th count was reached. Similarly 1-Imix, 2-Imix, etc., seems to repeat the Imix day pointlessly. The point was to reach 13, when the Moon would have become full, or new, and simultaneously keep up a rotation through the twenty day names, each of which attributes some quality to the particular day. The result, at any rate, was to have a calendar with 260 separate names for each day of the year.

A Person: 20 digits and toes (day names)
13 Day Numbers (20 x 13 = 260 days)
9 Lords of the Night

The question also occurs, why was this 260-day calendar kept in use when the length of the year and the period of the Moon changed one hundred and fifty years later in 2193 BC, and again in 1492 BC, and then in 747 BC? There could be a number of reasons, but primary is the fact that the Tzolkin calendar, and the later Haab calendar, do not function as we would imagine a calendar to function, that is, as a sequence of numbers which have a one-to-one correspondence to the sequence of days, and are discarded just as the days are irretrievable once they have moved into the past. The Tzolkin has a different function to a people whose language base does not include a strong sense of time as a path, but who do have a heightened sense of space and geography. In Mesoamerica, time had a spatial quality, and the Tzolkin functioned as a map to the domain of time.

I also think that the Tzolkin was kept for the same reason that the I Ching in China (dating from the Shang era or before) was never abandoned, even surviving the book burning of 213 BC. If the Maya or Olmec were at all like other people throughout the world, they would believe that all their fortunes and failures in life were predetermined. The only glimpse into the future was to "read" the qualities of each day, for like fate, each was different from any other (and Tzolkin/Haab day-name combinations do not repeat for 52 years). Using the Tzolkin as a guide to life was not unlike contemporaneous Chinese use of the I Ching, or Mesopotamian and Indian astrology. Even if the number of days in the year changed and a more rational calendar were to be adopted, the Tzolkin would have to remain in use without interruption.

Modification of the Tzolkin

After 2193 BC the year went to 270, 275, or 280 days. The Tzolkin could easily accommodate the 280-day year by adding an additional rotation of 20 days. I suspect, however, that the year changed to 273 days. By chance, the Tzolkin could also accommodate a year of 273 days, since it would only slip behind by a count of 13 days every year. [note 6]

That the calendar fell out of sync with the Solar year did not matter as long as the Tzolkin's primary purpose was to determine the quality of the days of the year. Consider also that the rotation through the twenty day-names had already been in use for 800 years. Certainly, too, it was kept because it represented high science to the Olmecs.

This science of the Tzolkin was used in the control of the Gods and spiritual powers. Specifically it was eventually used to control the travels of the Sun. This theme resounds through all of the history of Mesoamerica, and was repeatedly proven in the future to be correct and effective.

I suspect another cycle which has come down to us, a count of 819 days assigned in rotation to each of the cardinal points, was added in this era. Researchers have been unable to make anything of this cycle, except to note that 819 is the product of 7, 9, and 13. The period of 819 days revolved through the four cardinal directions.

Linda Schele and David Freidel, in A Forest of Kings (1990), note that in Maya texts the God K (also identified as God G-II), who clearly is Mars, is associated with the four directions. We therefore need to look to Mars.

First, let's note that 819 days happens to be exactly three times the length of the year (273 days) at this time (3 * 273 = 819).

The orbital period of Mars was 720 days. This has been proposed by Donald W. Patten and Samuel R. Windsor, in The Mars-Earth Wars (1996), for the purpose of their model, and as related to the period before 747 BC. From my use of this orbital period value, it appears to be correct.

In the era of 3147 BC to 2349 BC, the synodic period of Mars would have been (720 * 240) / (720 - 240) = 360 days. Thus Mars would show up in the same location of the sky every three years of 240 days, 2 * 360 - 3 * 240 = 0 (and once every year and a half). This three-fold repetition of the calendar year is, of course, also reflected in the mysterious 819 days, as already noted.

Let me suggest the following as a history of this: After 3067 BC (when Mars first started to appear near earth), with the year at 240 days, the reappearances of Mars were marked, correctly, at 3 intervals of the 240-day year, 720 days. This was the index of possible catastrophic interactions with Mars, which was good until about 2750 BC, after which Mars no longer was seen near Earth.

After 2349 BC, when the year went to 260 days, three of the 260-day periods were used instead, 780 days. This was incorrect and may have been useless in predicting catastrophes, but that did not matter, for Mars had disappeared from consideration some 400 years earlier, and by the end of the previous era it was probably no longer recalled why Mars had been assigned to one of the cardinal directions at intervals of three calendar years.

After 2193 BC the year went to 273 days. The assignment of Mars to the four cardinal directions was accomplished on a rotation of three years of 273 days, adding up to 819 days. Even if nothing happened, it did not matter. The interval of three years, tied to the four cardinal directions and the planet Mars, was a formal part of calendar computations, and had nothing to do with the close appearances of Mars.

The predictive value of the 819 day cycle was still correct when in 1935 BC Mars again made a series of destructive approaches. We could guess that, because of the circular nature of orbits, the interval was still 15 or 30 years, but of course years of 273 days. Mars would cruise close to Earth after every 5th interval of 819 days.

What then happened at 819-day intervals after that? It may have been kept at the value of 819 because in 1492 BC and 1442 BC a different planet, Venus, started interfering with Earth. The Mars cycle of 819 days remained unchanged. The next opportunity would have been in 1492 BC when the length of the year changed again. But no changes were made.

A Person: 20 digits and toes (day names)
13 Day Numbers (20 x 13 = 260 days)
819 days rotated against the four cardinal directions
9 Lords of the Night

The Haab Calendar

After 1492 BC the year changed to 360 days, and the period of the Moon changed to 30 days. This is certain from many sources throughout the world. A solution would have been to add five additional sets of 20 "name day" rotations ("months") to the Tzolkin, or to add five more numbers (from 13 to 18). But this would have been completely unacceptable, for the Tzolkin had to remain as it was, and as it had been for 1500 years. To extend the count would have been equivalent to changing our 7-day week to 9 days.

The only solution was a parallel calendar of 360-day period. This was done by starting a rotation through the names of 18 "months" (Uinals) of 20 days each, called the "Haab." Seven hundred years later this was augmented with 5 more days. Now for the first time we see a calendar instituted which has a familiar sensibility, like the numbered days of our months. The 18 months were separately named, but only 20 days were assigned to each month. The glyphs for the months are completely different from the Tzolkin glyphs and have the characteristics of the later development of the written language. A number of them also simply translate to "first," "second," etc. But the "months" -- that is, the Uinals -- still were 20 days long as they were previously, and were called "months" -- that is, a word meaning "moon." [note 7]

[Image: Haab Calendar]
[Image: The eighteen months of the Haab calendar plus the additional five-day period of the "sleep of the year," Uayeb. After Linda Schele and David Freidel "A Forest of Kings" (1990).]

The 20 day numbers were most likely modeled after the 20 day names of the Tzolkin. The 360-day calendar of 18 months of 20 days also makes no sense, since the actual (lunar) months were 30 days long, but it neatly filled the year, and every three calendar months (60 days) coincided with two rotations of the Moon.

The Tzolkin remained in use, arcane as it was, to determine the quality of any day, and determined the lot in life of a person named for a particular number-name day on which he was born.

The two calendars were entirely different, yet both were kept in use for 3000 years. (In some regions of Guatemala they are still in use today, even in printed form.) In the Classical era of the Maya, the days were identified as the number-name of the Tzolkin, followed by the number-name of the Haab. The two calendars of 260 days and 360 days would not repeat a combination of two names for 13 years.

A Person: 20 digits and toes (day names)
13 Day Numbers (20 x 13 = 260)
18 months of 20 days (18 x 20 = 360) (13 year cycle)
819 days rotated against four cardinal directions
9 Lords of the Night

The Haab Revised and the Long Count

After 747 BC the year changed to 365 and 1/4 days. The Olmec correction, like almost everywhere else in the world, was to add 5 unnamed days at the end of the year. For the Olmecs this was a 19th short "month" Uayeb of five days, called "the sleep of the year." Actually this would shift the year one day backwards in the solar year every 4 years, for it did not account for the quarter day left over. The revised calendar in Peru actually added a leap day every four years. Mesoamerica through Classical times did not, with the exception of the Zapotecs at Monte Alban (after about 400 or 200 BC).

In 747 BC the Olmec also started to count days, perhaps to recalculate the length of the year after the Earth shock of 747 BC. This is known as the "Long Count" which was carried into the future without interruption for the next 2700 years, but was mainly used by the Maya until about AD 900. The count started on February 28 of 747 BC (actually the Julian year of -748) with all measures set to zero -- zero days (Kins), zero months of 20 days (Uinals), zero "double-decades" of 20 Tun years (Katuns), and zero years of 360 days (Tuns). In our notation of these Katuns, Tuns, Uinals, and Kins, the Long Count is rendered as 0.0.0.0 February 28, -748.

This is also the date of the start of the Babylonian "Era of Nabonassar" (which starts at nightfall of February 27th), and the same calendar day after which the Romans restarted the year since the 8th century BC. [note 8]

A larger unit, called a "Baktun," consisting of 20 "Katuns," (400 Tun years of 360 days) was added at the same time or at a later date. A starting "Baktun" value of "6" was assigned to February 28 of 747 BC. The official Long Count date for February 28 -748 (using our dotted notation) thus reads "6.0.0.0.0 11-Ahau 8-Uo," where "11-Ahau" and "8-Uo" are the day names in the rotating Tzolkin and Haab calendars. (This is based on the August 11 correlation of Thompson.) The odd day-names, both located in the middle of the Tzolkin and Haab calendars, confirm that the Tzolkin and Haab were already rotating simultaneously before this time.

It might be possible to estimate from this when the Haab was first instituted, or what the general plan for the Haab was. Others have suggested that it is likely that the summer or winter solstice was used to celebrate the start of the year. But this notion reflects our contemporary reductionist calendar concepts. It also reflects our thinking that calendars should start at the first day of the first month. That is not at all certain.

Some people in Guatemala celebrate the New Year at the winter solstice, or at Christmas. This is when the Haab recycles for them. But it is the 9th month of the Haab. But it is also possible, as I pointed out above, that the Haab calendar and its later extra 5-day "month" were instituted without regard for an elegant design, and was arbitrarily added to the existing Tzolkin. [note 9]

What is of greater interest is to know how soon the Haab was corrected by adding 5 additional days. By the 18th month (of 20 days) after February 28, 747 BC, it would have been obvious that the year was now longer, and a 19th short month should be added. But since the Olmecs kept track of the setting position of the Sun by days of the Tzolkin and Haab, it is likely they had a much earlier indication of how many days the year had slipped behind.

The intercalated 5 days were added probably as soon as the first one of the longer years was about to pass. The traditional use of the Haab in the Classical era adds the extra five days after the 18th month, Cumku. In fact it was added at the end of the first new longer year, as can be confirmed from the current usage by the Chiapas (see below). Otherwise there would not have been the amazing simultaneous coincidence with the start of the Era of Nabonassar.

Verification that the 5 days were added after only one of the old years had lapsed, comes from the practices of contemporary upland Maya in Chiapas, Mexico, who retain a form of the Haab calendar today. The contemporary Haab calendar, in this instance, starts directly after Christmas, that is, a few days after the winter solstice. No accounting is made of the fact that the calendar will slip backwards against the Gregorian calendar. Somehow an extra day is added every four years.

The year starts with a Haab month which, from its name, is the equivalent to the ninth month of the older Haab of antiquity, and continues in sync with the Haab of antiquity. The second month of the contemporary calendar is the 10th month of the old Haab, etc. There is one exception. The intercalated 5 days are placed after the third month (of 20 days), not after the last month. The third month of 20 days ends on February 24. The intercalated days start on February 25 and conclude on the day after February 28. [note 10]

The use of the Long Count, and especially the starting value of 6 Baktuns, shows that an historical awareness had developed by 747 BC. Six Baktuns represent 2400 solar years stretching back in time to 3147 BC. The Olmecs figured the past on the basis of 360-day years, but the actual length of the year does not enter the basic calculation of when the current era started. A Tun was a solar year; the length did not matter.

The Long Count rotates through Tuns of 360 days (18 times 20), and all the future uses of the Long Count disregard the 365-day Tuns, and counted instead in 360-day Tuns. This is rather amazing, and probably confirms that the Long Count was started simply to measure the new number of days in the year.

Of course what we do is to use 365.24 days as the length of the year, and simply count backwards by days (called the Julian day count). Within a few hundred years after 747 BC, the Olmecs ended up doing the same thing, that is, using 365.24 days. The prior year length of 360 days used by the Long Count was ignored or forgotten.

That the Long Count was started in 747 BC is apparent also from the fact that 6.0.0.0.0 of the Long Count falls on February 28, 747 BC, but also from the fact that this date completes a Katun 11. Katuns are named after the last Tzolkin day of a Katun; in this case the day 11-Ahau. This last is significant when we know from the 16th century AD Maya Chilam Balam that all of pre-history always was assigned to Katun 11-Ahau.

Some 1400 years later, in circa AD 700, the Maya at the site of Palenque retrocalculate dates 3000 years earlier, and list them according to the notion that the past -- all of the past -- consisted of 365 day Haab years, not 360 day Haab years. The Maya (or their Olmec predecessors) also retrocalculated back to the very beginning of the current era (the "second creation") to find that the initial Haab and Tzolkin days name and numbers were 8-Cumku and 4-Ahau. This works for both the "August 11" and the "August 13" concordance.

What does not work in this retrocalculation, is finding a Katun 11 ending for the previous era. The previous era ends in 4-Ahau, and thus the previous Katun is named Katun 4-Ahau. Despite this, when the Chilam Balam (in Book 10) recounts events from before the start of the current era (before 3147 BC, but thought to be 3114 BC), they are listed as happening in Katun 11. The notion obviously is from the time in 747 BC, when the Long Count was instituted as a Katun 11 had just ended. See the chapter "The Chilam Balam Books."

A Person: 20 digits and toes (day names)
13 Day Numbers (20 x 13 = 260 days)
18 months of 20 days (18 x 20 = 360 days)
19th month of 5 empty days (= 365 days)
819 days rotated against four cardinal directions
9 Lords of the Night

Of course the rotating calendars make no sense. Only the Long Count makes sense. One could tell how far in the past an event had happened, but only in terms of months (Uinals), which fell short of a cycle of the Moon, and years (Tuns) which fell 5 days short of the solar year. A relationship to the solar year could be kept by celebrating New Year at the summer (or winter) solstice, although solstice dates are not easy to determine. In fact, none of the people of the Central Valley of Mexico or the Maya of Mexico or the Guatemalan Peten celebrated or marked a solstice date, with the exception of the Chiapas mentioned above who remodeled their calendar to fit a Christian liturgical feast day near the winter solstice.

The actual day-name and day-number of a New Year day would change with each year. In the Yucatan the Maya of the Classical era celebrated the new year on July 26, when the Sun passed directly overhead at the site of Edzna, as did the people of Teotihuacan in Central Mexico (circa AD 200).

The simultaneous rotation through the 260-day cycle and the 365-day cycle would repeat every named day combination only once every 52 years (actually 52 "tun years"). That was of course significant in that it reflected the "traditional" possibility of reaching the end of creation (the so-called "52-year Venus cycle"), as was initially determined in the period between 2349 BC and 2193 BC.

The 365-day year, without leap days added, also kept exact pace with the synodic period of Venus, which was probably much more important than any other considerations. As long as there was a strong interest in the movements of the planet Venus, it would make sense to not add the leap day, and retain the traditional calendars. The complex Tzolkin and Haab calendars spread everywhere in Mesoamerica, but the Long Count only saw wide use by the Maya.

The Katun Cycle

After circa AD 900 the Maya give up on the Long Count which had reached back 1500 years (4000 years if retrocalculated), and continue to use only a short cycle of Katuns -- 20 years of 360 days, about 19.7 solar years total for each Katun. Consecutive Katuns were collected in a repeating series of 13 Katuns (rather than the 20 Katuns constituting a Baktun), because the ending day-names of the Katuns repeat after 13 Katuns.

The cycle of 13 Katuns is approximately 256 solar years. This series is all the Maya retain of their calendar, 600 years after the collapse of their kingdoms -- plus, of course, the endlessly repeating assignment of days to the Tzolkin, the Haab, and the "Nine Lords of the Night."

Consecutive Katuns always are listed as starting with Katun 11, named after the last day, 11-Ahau, and are followed by Katun 9, etc., with the series of declining even numbered Katuns after the last of the odd-numbered Katuns, Katun 1. This is seen in use in the 16th century AD Maya Book Of Chilam Balam.

Others have suggested that this is because Katun 11-Ahau begins with 1-Imix, the first day of the Tzolkin. But in fact it is because a Katun 11-Ahau ends on February 28, 747 BC (-748), when the Long Count (6.0.0.0.0) was instituted (using the "August 11" correlation). Katuns are named after the name of the last day of the Katun period, not after the day with which they start (as we would do). It was always the completion of a time period, not the beginning, that mattered. For the Maya, unlike for us, a period of time did not exist until it was completed; it also did not exist yet while it was still ongoing.

The Four Ages

The concept of "suns" or "sun ages" was recognized throughout Mesoamerica by various peoples, as well as by people in many other parts of the world. (And has become a big deal among catastrophists.) These ages are meant to represent various creations of the world, or recreations after a catastrophic destruction. In Mesoamerica four ages were recognized by all except by the Toltecs and the Aztecs, who claimed that the world had been recreated five times. Both of these people held their own invasion of the Valley of Mexico as the last recreation of the world.

The creations and recreations can be pinpointed, but the series of dates runs into conflict with various concepts of what constitutes a new age.

The Olmec and Maya Long Count calendar starts the "current creation" in (the retrocalculated year of) 3114 BC. This date does not count the two destructions of the Earth since that time, but only recognizes that conditions on Earth and in the skies were completely different before and after. This was known as the "second creation," and from this two ages are recognized.

Book 10 of the Maya Chilam Balam books places creations or recreations after floods, and thus recognizes three eras, the periods before and after 3114 BC, and the period after 2349 BC, this last started with an event known as the "third reign" or what would be the "third creation." But the dark skies after 1492 or 1440 BC are also dealt with as the start of a new creation. It is not surprising that this confusion exists, since Book 10 of the Chilam Balam is obviously derived from diverse sources.

The concept of "four ages" is a satisfying shorthand if we associate a change of the length of the year with each of the ages, and especially if these events can be associated with some worldwide catastrophe. But it does not work out that way. What can be gathered from the most reliable source, the Chilam Balam, is the following:

The fall of the Absu, the end of the "third creation," is noted as "the second baptism" with the implication that the first is the flood of 3147 BC (which is also mentioned). The Chilam Balam also implies the start of a new calendar. In this it parallels the Chinese Annals of Shu, as well as the Babylonian Enuma Elish.

There is also a reference to "walking in darkness," which can be identified as the 40 years or so after the contact by Venus in 1492 BC. The Israelites also "walked in darkness."

"Then they perceived that the world was being created. Then creation dawned upon the world."

The reference to creation is suggested for 1492 BC by its placement in the texts, but could also refer to the 200-year climatic downturn experienced worldwide after 2193 BC.

I suspect that the Chilam Balam was transcribed from books indigenous to the Peten and Yucatan Maya. The story of these books may have differed from the records kept among the Olmecs of Veracruz and in the Valley of Mexico, which have not survived.

But we can count four ages from Olmec sources under a completely different paradigm: the site alignments used in the Olmec coastal area since 1440 BC, and in the Valley of Mexico since about 600 BC.

These horizon alignments for sunrise or sunset reference four dates. First, starting at San Lorenzo and followed by almost every later site, the date of April 19, 1492 BC is recalled in the alignment of the setting Sun to some mountain or volcano. Apparently when San Lorenzo was established, the horizon location of the setting Sun for that date was known.

Similarly, at La Venta the alignment for February 28, 747 BC was also known, since it was experienced. After 747 BC the date of August 12, 3114 BC, was calculated with the aid of the newly developed Long Count. Various dates centering on July 685 BC, were also experienced and incorporated into the alignments of sites after 685 BC.

Last, in about AD 200, and at some locations, both since before and directly after 685 BC, the setting of the culmination of the Pleiades is used to signal the event of 2349 BC. These alignments show up at all later sites. The alignments are discussed in the chapter "Olmec Site Alignments."

Endnotes

Note 1 --

The dotted notation, used by archaeologists as a shorthand to identify the Long Count, consists from left to right of measures known as Baktuns, Katuns, Tuns, Uinals, and Kins.

These are thus written in modern form as as Baktun (dot) Katun (dot) Tun (dot) Uinal (dot) Kin. A dotted notation is always followed by the Tzolkin day number and day name combination plus the Haab day number and month name combination.

Note 2 --

For Long Count dates which were retrocalculated by the Maya in circa AD 700 at Palenque, as well as the correction of the Katuns (where I have supplied the Baktun) of Book 10 of the Chilam Balam, a correction should be used. This will be based on the suspicion that there did not exist a record in actual Long Count days for events before 747 BC, but only a listing by Katuns and Baktuns. This correction is easy to do: Since 6 Baktuns were added to the dotted date of 0.0.0.0, the starting date of the current era would have been 2400 years earlier (6 times 400), and thus 747 BC less 2400 years: 3147 BC.

The start of the yet earlier era would be 3147 BC less 13 times 400 years: 8347 BC.

For the inscriptions at Palenque the correction should be based on the fact that the Olmecs knew that the era prior to 747 BC represented years of 360 days, not 365.24 days. But this was long forgotten 1400 years later when the Maya of Palenque start carving monumental inscriptions. Our calculations and those of the Maya of Palenque are based on a 365.24-day year, and would be off by 5.24 days per year before 747 BC, that is, the dates we use are placed too far into the past. The correction is (3114-747) * 5.24 / 365.24 = 34 years.

So, for example, when in AD 700 the Maya at Palenque retrocalculated a date of 2360 BC for some event listed among the inscriptions, it was based, like our calculations, on a 365.24 day year, and would be too far into the past by (2360-747) * 5.24 / 365.24 = 24 years. The date should be 2336 BC.

The Maya were perfectly capable of calculating backwards, and making allowances for the extra 0.24 day of the year. Anthony Aveni, in Skywatchers of Ancient Mexico (1980), notes a number of instances among Maya inscriptions (at Copan) where successful attempts were made to indicate the length of the tropical year. The Maya ended up with a year of 365.2420 days, only 0.0002 days different from the current value of 365.2422 days.
[return to text]

Note 3 --

See the chapter "The Chilam Balam Books" for a retelling of the creation of the world which dates back to thousands of years before 3114 BC and was apparently transcribed from Maya tree-bark codexes. Other pages of the Chilam Balam describe the darkness of the Younger Dryas (10,900 to 9,000 BC), and hint at yet earlier ages dating to the equivalent of the European Magdalenian period (17,000 to 14,000 years ago) or earlier (I suspect to 41,000 years ago).
[return to text]

Note 4 --

The Maya (and Olmecs) used a base-20 in their commerce, but it is difficult to maintain that they also did so with their calendar, as is often maintained. The "units" of the Long Count do not all advance as powers of 20, since the Uinals advance when reaching 18, not 20. Baktuns cycle at the number 13. The number 20 just happens to be a larger unit to count in, like our dozen or hundred. The glyphic representation is certainly in base-5.
[return to text]

Note 5 --

Although some of what I have suggested is conjecture, I should note a remarkable similarity of the Mesoamerican 20 day names and 12 day numbers to the calendar of the Chinese Shang dynasty, after about 1400 BC, which rotated 10 "celestial day names" (instead of 20) against 12 "earthly day names" to produce a similar calendar (of 60-day periods), elements of which lasted well into the current era. The Chou dynasty extended the rotation of 60 day names to the names of years. This last persists today.

Although the Shang dynasty is much later than the period under discussion here (before 2349 BC), it would not be at all surprising if the Shang calendar represented a holdover from an earlier period, when the 240-day year was divided into four seasons of 60 days each, thus a total of 240 days. China experiences four distinct seasons; Mesoamerica experiences a completely different cycle of seasons. The Shang, at any rate, added the lunar month days to the 60-day periods to furnish nearly accurate calendar dates during the year.
[return to text]

Note 6 --

I suggest a year of 273 days, based on conjectures developed later in this text. Since 273 is 13 days more than 260 days, the Tzolkin could have been expanded by adding one round of 13 numbers, or the calendar could have been left to slip backwards 13 days per year. The reason for selecting the second might have depended on an initial attempt to keep the calendar in line with the half-moon periods of the previous era. This did not work out, for the Moon changed to a period of 27 or 28 days after 2193 BC, which we know from (later) Shang oracle records.
[return to text]

Note 7 --

It is possible that the Haab was devised separately by a people different from those who devised the Tzolkin, and the two calendars were kept after a cultural merger after 1500 BC.
[return to text]

Note 8 --

According to Ussher, the era of Nabonassar starts at noon of February 26th, thus actually on the 27th. Ussher writes:

"From twelve o'clock, on the first day of the Egyptian month Thoth, from Wednesday, February 26th, in the evening, in the year 747 BC, all astronomers unanimously start the calendar of Nabonassar."

-- James Bishop Ussher, Annals of the World (AD 1650)

Additionally, because of the Mesoamerican concepts that a day does not exist until it is completed, the Long Count use of "day zero" actually signifies the first day of the new era, so that the actual era-ending date is February 27th.
[return to text]

Note 9 --

The short five-day month can be neglected in any retrocalculation here, because it was instituted in 747 BC. If we take a hint from how the Olmecs dealt with other calendar adjustments, it would suggest that the Haab was instituted the day after the completion of the cataclysm of 1492 BC. From an earlier chapter we know that this happened on a Gregorian equivalent calendar date of April 19. (Bible tradition, for the start, is April 17th.)

On February 28, 747 BC, the Haab day fell on 8-Uo. This is the 29th day of the Haab. Thus, in 747 BC, the annual secular calendar, which starts with 0-Pop, had started 29 days earlier in that year, equivalent to January 30 on an equivalent Gregorian calendar. Thus, between April 19, 1492 BC and February 28, 747 BC the Haab had slipped 80 days backward, which is four 20-day Uinal months. This number is not in any sense meaningful.

Alternately, taking into account the fact that before 685 BC the winter solstice fell some 15 days earlier, on December 8, the Haab would have restarted 53 days after the winter solstice. Except for the fact that 53 days represents a 52-day interval, this also is such an arbitrary figure, that it can only be suggested that there was no relationship between the Haab and either the winter or summer solstice.

Vincent H. Malmstrom, in Cycles of the Sun, Mysteries of the Moon (1997), dates the first use of the Haab to 1324 or 1321 BC, based on placing the day 0-Pop (the first day of the Haab) at the summer solstice. The calculation would only be in error by 8 years, since the extra five days have to be subtracted from the Haab for the period before 747 BC. But also it is absurd to think that a beginning date (0-Pop) would be at all meaningful in Mesoamerican chronology.

The usage of the Chiapas (see other endnote below) might bear out Malmstrom's conjecture that the New Year (the start of the Haab) was celebrated at the summer solstice, even though the Chiapas today start the year with the winter solstice (actually at Christmas), for they start with the ninth month (Uinal) of the traditional Haab calendar. The name of the month which starts the Haab is clear from the fact that the names of the first few months of the Haab translate to "first," "second," "third," etc. That would place the beginning of the Haab 160 days before Christmas (8 completed months). This is not at the summer solstice, but 24 days later, on July 18.

When New Year is celebrated is a local option. The Maya, as with Teotihuacan, used July 26. In colonial times the Aztecs celebrated the start of the new year on February 26. (There are some discrepancies with respect to this particular date, however. See the endnotes to Appendix B, "Celestial Mechanics.")
[return to text]

Note 10 --

See Gary H Gossen, "A Chamula solar calendar board from Chiapas, Mexico," in, Norman Hammond, editor, Mesoamerican Archaeology (1974). Although the Tzolkin was held as sacred, the Haab was apparently adjusted to start as convenient by various tribes.
[return to text]

Calculations are in Unix bc notation, where ^ denotes exponentiation; the functions a(rctangent), s(ine), and c(osine) use radians; angle conversions to radians or degrees by the divisors rad=.017+ and deg=57.2+; other functions are shown as f( ); tan( )=s( )/c( )
units: million == 1,000,000; billion == 1,000,000,000;
AU == 93,000,000 miles.

[previous] [table of contents] [next]

URL of this page: http://saturniancosmology.org/maya.php
This page last updated: Sunday, April 30th, 2017
Size of this page: 12546 words.

Feel free to email me with any comments or corrections. Find an email [address] here.

Copyright © 2001 - 2024 Jno Cook

Permission to reprint in whole or in part is granted,
provided full credit is given.